W4: Physician Agency
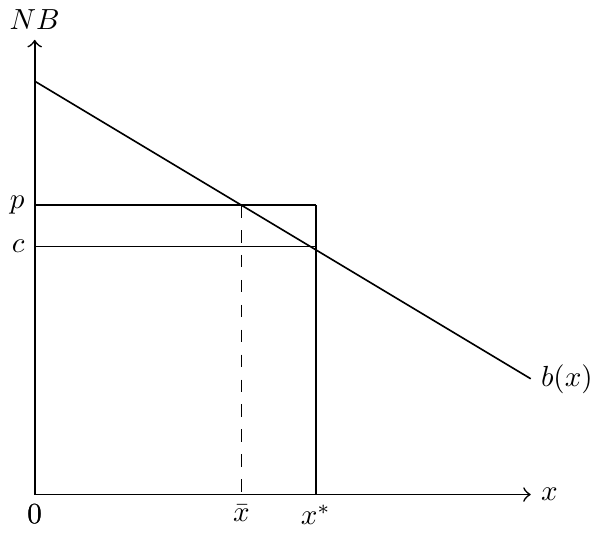
Denote the quantity of care consumed by \(x\), and denote by \(B(x)\) the function that determinesthe benefit of care to the patient. Assume that the patient must pay the full price of care, \(px\), so that their net benefit is \(NB=B(x)−px\).
Question 1:
Find the patient’s optimal \(x\).
The patient just wants to maximize their net benefit, \(B(x) - px\). Taking the derivative and setting to 0, this means \(B'(x) = p\) (i.e., marginal benefit to the patient is equal to the patient’s marginal cost).
Question 2:
Draw the marginal benefit on a graph and note the price and patient’s optimal quantity.
Question 3:
Find the physician’s optimal \(x\) assuming \(NB^{0}=0\).
The physician is profit maximizing, subject to the constraint that \(NB^{0}=B(x) - px=0\). Plugging this constraint into the profit function yields, \(\pi = B(x) - NB^{0} - cx = B(x) - cx\). Taking the derivative and setting it to 0 yields the expression, \(B'(x)=c\). So the physician also set’s marginal benefit equal to marginal cost…they just focus on their own marginal cost instead of the marginal cost to the patient.
Question 4:
Add the physician’s optimal \(x\) to your graph and interpret the difference.